康瑞部落

早期推文中介绍了Elf：基于擦除的浮点压缩算法，对于双精度浮点数的压缩有着很高的效率，尤其在压缩率方面相比Gorilla和Chimp₁₂₈分别提高了50%和13%。观察到时间序列中的值通常有着相似的有效值位数，因此Elf算法有进一步的优化空间。本次为大家带来重庆大学时空实验室基于VLDB 2023工作《Elf: Erasing-based Lossless Floating-Point Compression》的扩展论文《Erasing-based lossless compression method for streaming floating-point time series》。此工作目前正在被数据库领域国际顶级期刊VLDBJ审稿中。值得一提的是，重庆大学时空实验室团队已对Elf+和Elf相关算法申请了中国专利和美国专利，欢迎产业界随时合作。 

一．背景

生产实践中产生了海量的浮点时间序列数据，亟需一种有效的方法在传输和存储之前对时间序列数据进行压缩。通用压缩算法虽然可以达到很好的压缩比，但时间开销很大。有损压缩算法会丢失一些信息，不适合科学计算、数据管理等关键场景。基于异或运算的无损压缩算法成为主流，如Gorilla和Chimp，尽管都有着不错的压缩效率，但仍未充分利用尾随零。基于此，重庆大学时空实验室团队提出了Elf算法，通过计算有效值位数β对浮点数v的尾数进行擦除，从而形成大量的尾随零，并存储擦除值与前值的异或结果用于解压缩（如图1所示）。同时Elf改进了异或结果的编码策略，进一步提高了压缩效率。有关Elf的详细介绍，请参考Elf：基于擦除的浮点压缩算法。

通过观察发现，时间序列中的值通常具有相似的有效值位数β，因此它们的修正有效值位数β^*也是相似的。图2显示了论文用到的22个数据集中两个连续值的β^*的相等情况和不相等情况的比率，从中可以看出，几乎所有数据集的相等情况远多于不相等情况。

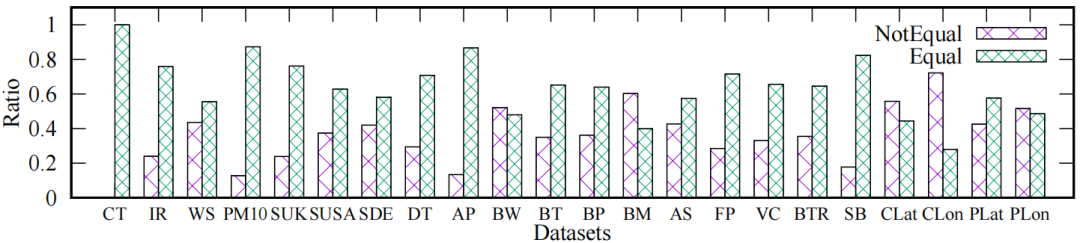
在Elf算法中，如果要擦除值v，需要使用4bits来记录它的β^*。一种可能优化的方法是记录时间序列的全局有效值位数β_g^*，每个值v的有效值位数β^*都可以用β_g^*表示。然而，这种方法存在几个缺点。首先，在压缩时间序列之前，需要知道β_g^*，这通常在流式传输场景中无法实现。其次，当β^*大于或小于β_g^*时，可能会导致有损耗的压缩或不充分的压缩。

为此，论文提出了Elf+，最大限度地利用前一个值的修正有效值位数β_pre^*。此算法不仅适用于流式场景，也适用动态有效值位数的要求，并且保留了无损压缩的特性。

二．方法介绍

2.1 总体框架

图3显示了Elf算法的总体框架，由擦除器、压缩器、解压器和恢复器组成。Elf+在Elf的基础上对擦除器的修正有效值位数β^*的编码策略进行了优化。

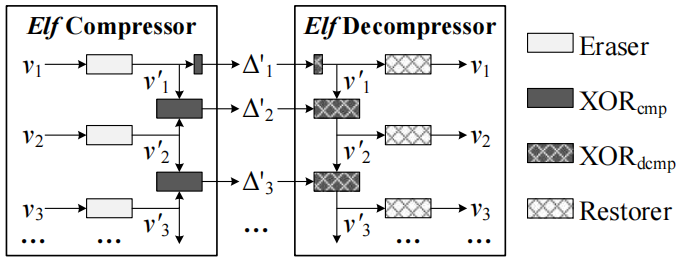
2.2 Elf+擦除器

通过以下方式优化修正有效值位数编码。

（1）利用前一个值的β_pre^*：如果Elf擦除算法中的三个条件（即C₁：β^* < 16，δ≠ 0且52 − g(α) > 4）同时成立，进一步检查当前值的修正有效值位数β^*是否等于前一个β_pre^*。

如果β^* = β_pre^*，不再使用4bits写入β^*的值，而是只写入标志位“0”，因为可以从β_pre^*中恢复β^*，由此节省了3bits。

如果β^*≠ β_pre^*，写入标志位“1”，然后再写入4bits的β^*。因此，原Elf的擦除器（如图4(a)所示）转换为图4(b)所示的擦除器。

假设时间序列中β^*相等情况的比率为r_e。设r_e× 3－(1－r_e) > 0，则r_e > 0.25。也就是说，相等情况的比率大于0.25时，可以通过上述优化来保证正增益。由上文图2可知，所有实验数据集都满足这一条件。

（2）重置标志位：对于大部分数据集，在图4(b)的三种情况中，“C₁且β^* = β_pre^*”的情况所占比例最大，但使用了2bits（即“10”）来表示这种情况。根据编码理论，更频繁的情况需使用更少的比特进行编码。因此，在图4(b)中交换情况“C₁且β^* = β_pre^*”和情况“非C₁”的标志位（即“10”和“0”）。最后，擦除器的优化结果如图4(c)所示。

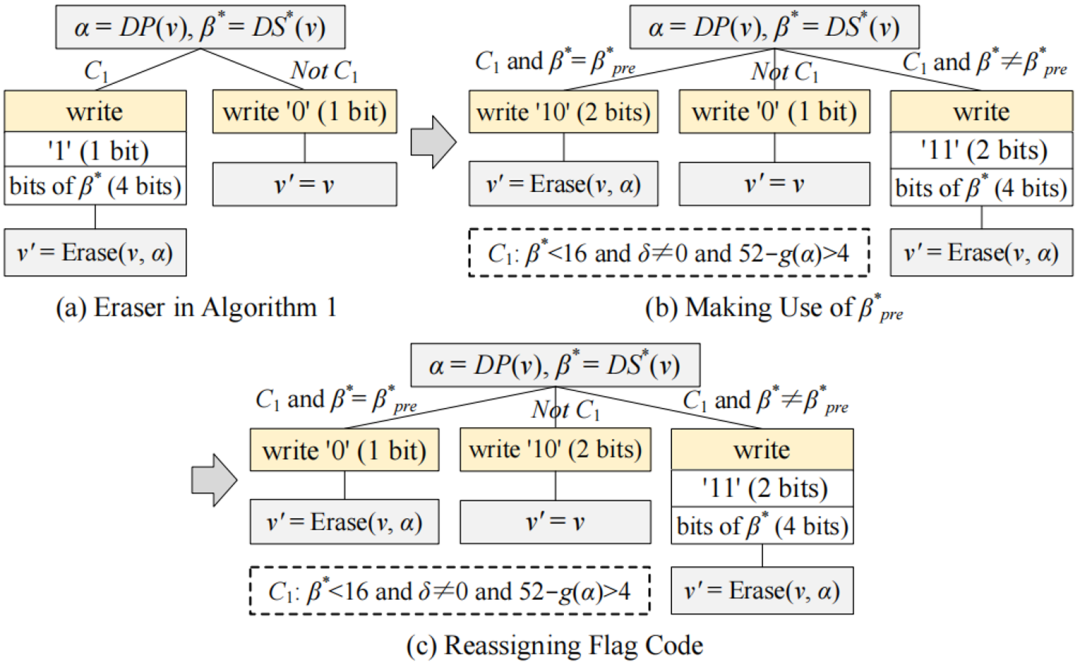
（3）擦除算法：算法3给出了Elf+尾数擦除过程的伪代码，与图4(c)中的3种情况一一对应。

2.3 Elf+恢复器

相应地，Elf+恢复器需要做一些调整。如算法4所示，首先从输入流in中读取一位标志位。如果标志位等于“0”，则意味着β^* = β_pre^*，故将β^*设置为β_pre^*，从解压器中获取擦除值v^’，并根据β^*从v^’恢复为v（第1-3行）。

如果标志位不等于“0”，将进一步读取一位标志位。如果新的标志位等于“0”，直接从中输入流in获得v（第5行）。否则，通过从输入流in中读取4bits来获得β^*，从解压器中获得擦除值v^’，并根据β^*从v^’恢复为v，同时需要更新β_pre^*以解压缩下一个值（第7-8行）。

2.4 Elf+压缩器与解压器

Elf与Elf+使用相同的压缩器与解压器。

2.5 实现细节

（1）计算有效值位数β：在代码实现过程中，Elf压缩最耗时的步骤是计算浮点数的有效值位数。最简单的方法是将浮点数转换为字符串，通过扫描字符串来计算，但数据类型转换开销大。再者，如Java中的BigDecimal，由于其实现了许多复杂但不必要的逻辑，这些逻辑不适用有效值位数的计算，因此性能更差。

Elf中的实现。根据Elf擦除器中的等式β = α + SP(v)+1，欲计算α，先循环检查条件“v × 10ⁱ= ⌊v × 10ⁱ⌋”是否成立，其中参数i根据SP(v)的值递增。首先使条件“v × 10ⁱ= ⌊v × 10ⁱ⌋”成立的参数i（假设为i^*）可以被视为小数位数α。最后，根据上述等式得到有效值位数β =i^*+ SP(v)+1。

Elf+中的实现。条件“v × 10ⁱ= ⌊v × 10ⁱ⌋”的验证所需要的时间复杂度为O(β)。为了加快这一过程，论文充分利用了时间序列中大多数值具有相同有效值位数的条件。如算法7所示，基于等式β = α + SP(v)+1，从i = max(β_pre^*－SP(v)－1, 1)开始验证，再分两种情况：

1）情况1，β ≤ β_pre^*。如果条件“v × 10ⁱ= ⌊v × 10ⁱ⌋”不成立，不断增加i，直到条件得到满足（第2-3行）。

2）情况2，β < β_pre^*。如果条件“i > 1及v × 10ⁱ= ⌊v × 10ⁱ⌋”成立，不断减小i，直到条件不满足（第4-5行）。

最后，根据等式β =i + SP(v)+1（第6行）获得有效值位数β。

因为时间序列中的值具有相似的有效位计数，算法7的时间复杂度预计为O(1)。

（2）计算有效值起始位置SP(v)：在代码实现过程中，另一个耗时的操作是计算v的有效值起始位置SP(v)。Elf直接通过公式SP(v) = ⌊log₁₀|v|⌋进行计算，然而，对数运算的开销相对较大。Elf+利用两个有序的指数数组来加速这一过程，即logArr₁ = {10⁰, 10¹, …, 10ⁱ, …}和logArr₂ = {10⁰, 10^-1, …, 10^-j, …}。首先顺序地扫描这两个数组。如果v > 1且10ⁱ ≤ v ≤ 10ⁱ⁺¹，则SP(v) = i；如果v< 1且10^-j ≤ v ≤ 10^-(j-1)，则SP(v) =－j。论文设置此指数数组长度均为10，可以满足大多数时间序列的要求。如果v ≥ 10¹⁰或v ≤ 10^-10，则调用SP(v) = ⌊log₁₀|v|⌋进行计算。

2.6 单精度浮点数的压缩

由于单精度浮点数的底层格式只有32位，包括1位的符号位、8位的指数部分和23位的尾数部分，故擦除算法、压缩策略中的参数也要做相应的调整。具体可见代码。

三．实验

论文在Elf实验的基础上，加入了Elf+算法。实验数据默认为双精度浮点数。

3.1 Elf对比Elf+  

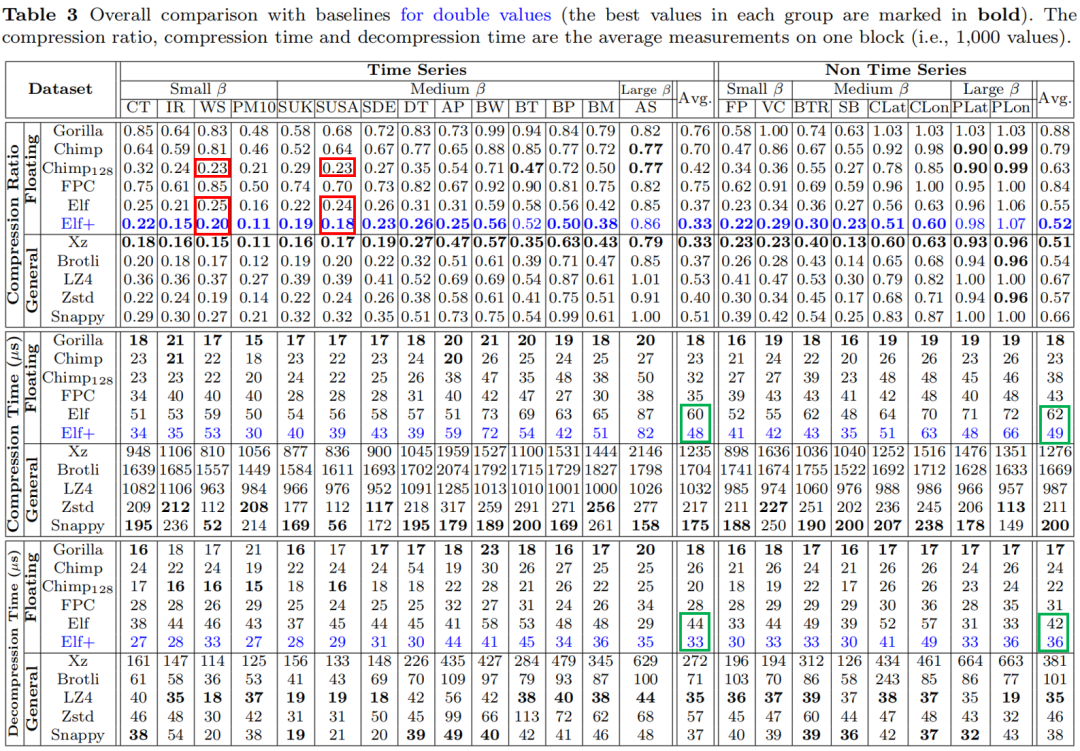
表3显示，对于具有小β和中β的时间序列和非时间序列，Elf+在压缩比方面总是比Elf表现得更好。这是因为Elf+基于时间序列中大多数值具有相同有效值位数的情况，使用更少的比特对β^*进行编码。这种优化使得Elf+在数据集WS和SUSA中甚至优于最佳竞争对手Chimp₁₂₈。

对于几乎所有的数据集，Elf+在压缩和解压缩过程中花费的时间都比Elf少，就平均而言，Elf+只有Elf压缩时间的79.5%，而解压时间的这一比例变为80.2%。这表明利用上一个值的修正有效值位数β_pre^*和创建对数数组能显著提高效率。

3.2 Elf+相比Chimp₁₂₈的效率提升

在Elf假设的数据传输场景中当传输速率小于6.17 ×10⁷ bits/s时，Elf的总体性能优于Chimp₁₂₈。Elf+与Chimp₁₂₈相比时，这一传输速率提高到了1.96 × 10⁸ bits/s。在典型的CS架构中，一个连接的带宽很少超过6.17 ×10⁷ bits/s（更不用说1.96 × 10⁸ bits/s了），且对于每个连接，Chimp₁₂₈将分配33KB的内存，这对于高并发场景是负担不起的。

3.3 不同β值的性能表现

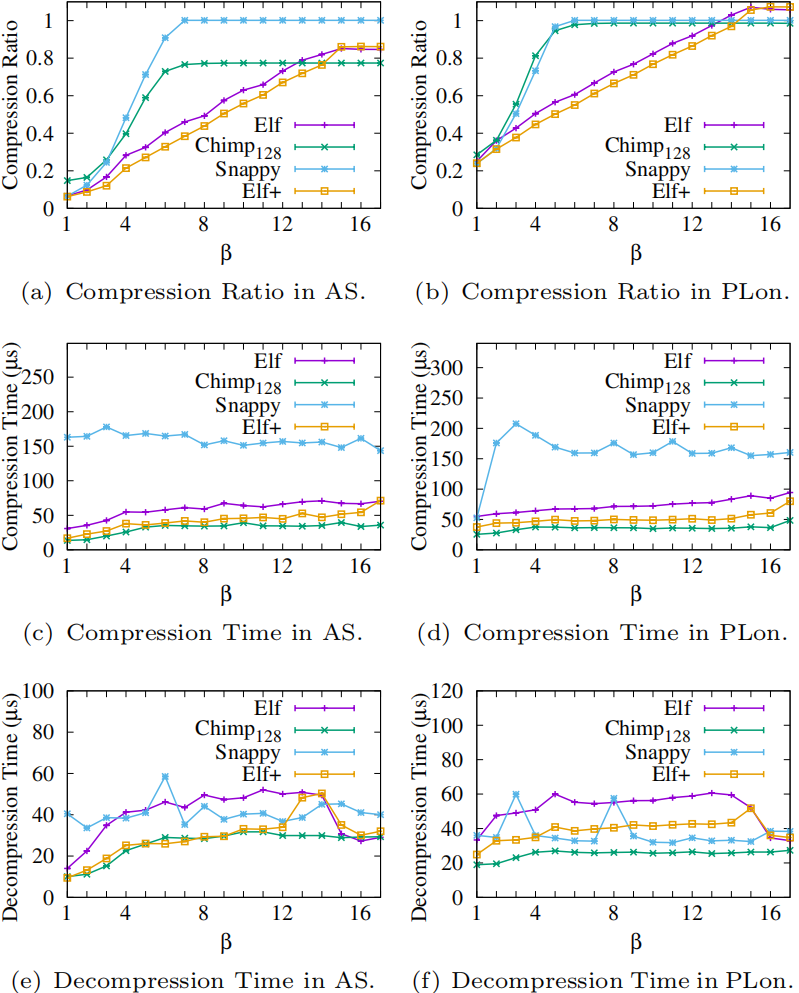
为了进一步研究β的影响，通过逐步减少时间序列数据集AS和非时间序列数据集PLon的有效值位数β进行了一组实验，并选择Chimp₁₂₈和Snappy作为基准。

如图5所示，β在3和13之间时，相比于Chimp₁₂₈和Snappy，Elf总是保持最好的压缩比。Elf+的压缩比趋势与Elf相似，且β < 15时，Elf+在两个数据集上的表现总是优于Elf。当β ≥ 15时，Elf+的表现略差于Elf，因为Elf+使用2bits来指示不进行擦除的情况，而Elf只需要1bit。

在压缩时间和解压缩时间方面，Elf+也有和Elf相似的趋势，但所需时间更少。

3.4 单精度值的性能

论文还进行了一组实验来验证Elf+算法在单精度值上的压缩性能。实验只使用β ≤ 7的数据集，因为单精度值的有效值位数不大于7。由于FPC不提供单精度值的版本，无法进行比较。

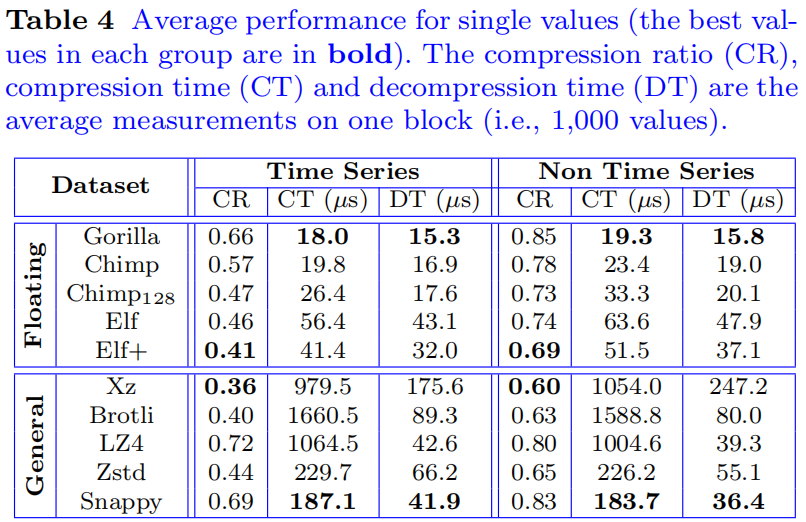
如表4所示， Elf+仍然是所有浮点压缩方法中在压缩比方面最好的。具体而言，Elf+在时间序列数据集和非时间序列数据集中的平均相对压缩比，与Chimp₁₂₈相比，分别提高了12.8%和5.5%。此外，与一般的压缩算法相比，Elf+比大多数算法（即LZ4、Zstd和Snappy）具有更好的压缩比，并且所消耗的时间显著少于所有算法。

与双精度值一样，Elf+在单精度值的压缩比、压缩时间和解压缩时间方面都优于Elf。

四．总结

论文在基于擦除的无损浮点压缩算法Elf的基础上，通过有效值位数优化和有效值起始位置优化，提出了一个升级版本Elf+。使用22个数据集进行的大量实验验证了Elf和Elf+在双精度值和单精度值方面的强大性能。特别地，对于双精度值，Elf的平均相对压缩比分别比Chimp₁₂₈和Gorilla提高了12.4%和43.9%。此外，Elf+的性能明显优于Elf，平均相对压缩比提高了7.6%，压缩时间效率提升了20.5%。

-End-

本文作者 朱明辉 重庆大学计算机科学与技术专业准研究生，重庆大学START团队成员。主要研究方向：时空数据挖掘

时空艺术团队（START，Spatio-Temporal Art）来自重庆大学时空实验室，旨在发挥企业和高校的优势，深入探索时空数据收集、存储、管理、挖掘、可视化相关技术，并积极推进学术成果在产业界的落地！年度有2~3名研究生名额，欢迎计算机、GIS等相关专业的学生报考！