康瑞部落

在物联网场景中，大量的浮点时间序列数据以流的方式生成，并在有限的带宽内传输，用于实时分析。为了提高效率，在传输前可以对数据进行压缩。但现有的浮点压缩方法要么是延迟较长的批处理压缩，要么是允许一定误差情况下压缩率差强人意的流式无损压缩。这两类算法都无法同时适应实时性要求和高压缩率要求。本次为大家带来重庆大学时空实验室和京东智能城市研究院联手在数据库领域顶级会议SIGMOD 2025发表的文章《Serf: Streaming Error-Bounded Floating-Point Compression》。

一. 背景

近年来，物联网得到了显著发展，传感器被分布在感兴趣区域的各个位置。如图1所示，在一个典型的物联网场景中，大量的浮点时间序列数据（简称时间序列）由各种传感器以流式方式持续生成，然后传输到服务器以进行进一步的实时分析和可视化。

图1. 流式误差有界浮点压缩的场景

这样的场景具有带宽有限、允许容错、有实时性要求的特点。而现有的时序数据压缩算法，可以分为三个主要类别：1) 批式无损压缩，2) 批式有损压缩， 3) 流式无损压缩。

批量无损压缩算法（例如，ALP）可以在不损失任何信息的情况下压缩时间序列，而批量有损压缩算法（例如，SZ 、MOST和 Machete）通常可以牺牲一些误差来获得更好的压缩率。这些批量压缩算法存在三个局限性。1) 采样率低的时候延迟长。它们需要等待批处理中的所有记录准备就绪，然后才能实际执行压缩操作。如果数据采样率较低，批量压缩将导致较长的延迟，这不符合上述实时性要求。2) 批量大小较小时性能较差。为了减少延迟，另一种解决方案是采用小批量技术，例如，将批量大小设置为小于50。然而，大多数批量压缩算法在面对小批量数据时的性能会急剧下降，因为它们难以发现记录之间的共享信息。3) 批处理中缓存记录的额外内存消耗。批量压缩算法需要在内存中缓存批处理中的所有记录，这可能会给边缘设备带来一定的压力，因为微型传感器设备的内存大小通常有限，注意这些有限的内存还需要支持某些程序的执行，例如压缩器和传输模块。

流式无损压缩算法可以在生成每条记录后立即对其进行压缩，同时保留所有信息。该领域中的几种最先进的方法，例如 Gorilla、Chimp 和 Elf ，都是基于对连续记录进行异或运算，因为时间序列中的连续记录通常变化不大，因此产生的异或值具有许多前导零或尾随零。然而，由于无损约束，当允许某些误差时，这些算法通常无法达到令人满意的压缩率。

据调研，目前还没有针对时间序列的流式有损压缩算法。流式有损压缩算法不仅解决了批量算法遇到的所有限制，而且与无损算法相比，实现了显著的压缩率。设计一种高效且紧凑的流式有损压缩算法将面临以下两个挑战。挑战一：如何在流式环境中实现具有误差界限保证的优秀压缩率？流式处理要求我们在每条记录生成后对其进行处理，这使得发现记录之间的共享信息变得困难。挑战二：如何在传感器有限的资源下确保高效率？注意传感器设备的计算和存储资源非常宝贵。因此，我们必须高效地处理数据，以避免堆积。

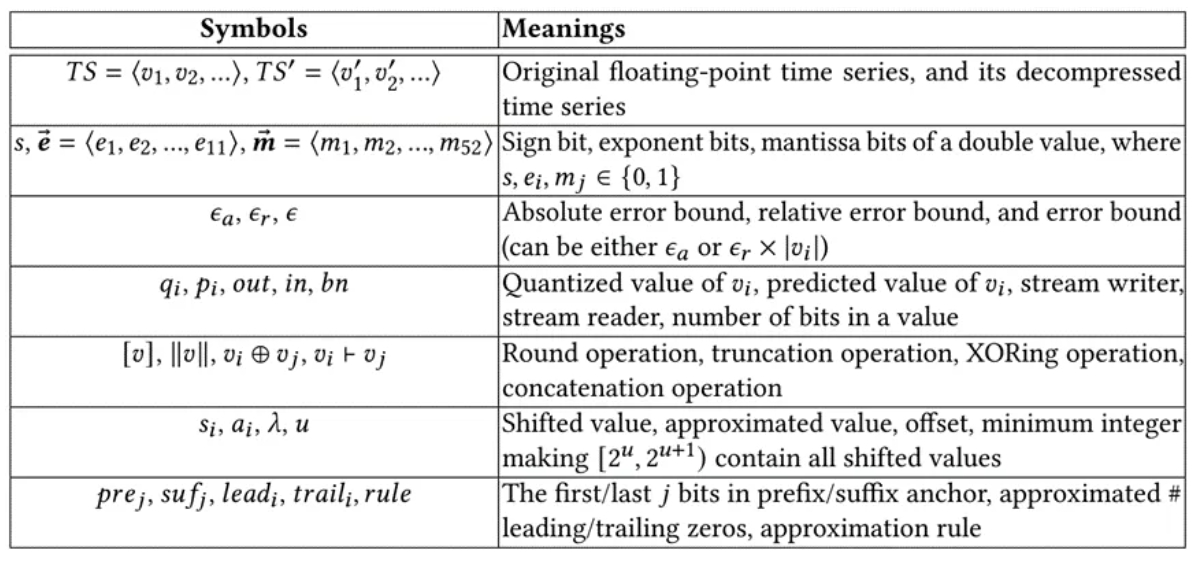
为了方便您的阅读和理解，给出下表：

表1. 文中符号及其含义

二. 方法介绍

2.1  基本方法Serf-Qt

Serf-Qt是一种基于量化的基本流式传输方法，其框架如图2所示。

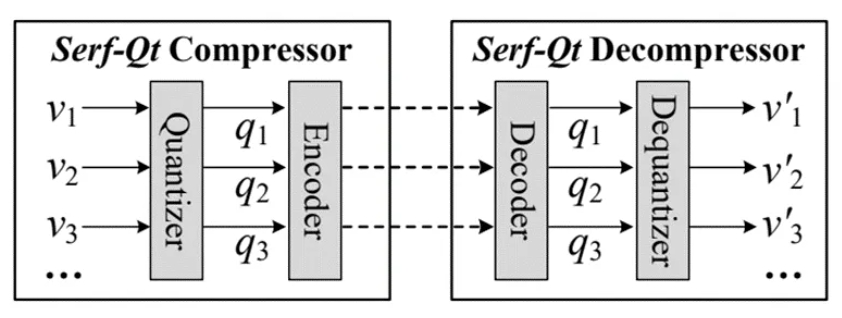
图2. Serf-Qt的框架

2.1.1量化器和反量化器

量化直接解释就是将浮点数值转换为整数，因为相比于浮点数值，整数更容易被压缩。假设原始数值为 ⟨v₁, v₂, ...⟩，量化后的整数为⟨q₁, q₂, ...⟩，量化器执行以下操作：

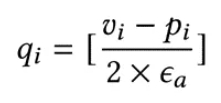
其中[*]是将浮点数值舍入为整数的运算，ϵ_a是用户给定的绝对误差界限，而p_i是v_i的预测值（见下一段)。

给定q_i，反量化器通过以下方式计算恢复值v′：

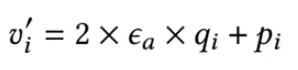
可以证明 |v_i−v_i′| ≤ ϵ_a，即恢复值v_i′ 严格满足绝对误差界约束。由于时间序列中两个连续的值通常变化很小，我们可以简单地令p_i= v_i-1′（我们可以在压缩和解压缩期间计算v_i-1′）。特别地，v₀′ = v₀ = 0。

2.1.2 编码器和解码器

现有的基于量化的压缩方法只能在批处理模式下工作，因为它们使用批处理策略对量化的整数进行编码，例如，Huffman编码或FSE（有限状态熵）编码。为了支持流式压缩，我们建议用流式编码器替换批处理编码器。具体而言，由于v_i和p_i之间的差异很小，即q_i倾向于分布在0附近，因此我们采用Elias gamma编码，这是一种自解释的流式编码方法，适合于压缩小数值。为了适应Elias gamma编码只能对正整数进行编码这一事实，我们首先基于Zigzag编码将q_i转换为正整数，然后使用Elias gamma编码对结果进行编码，即：

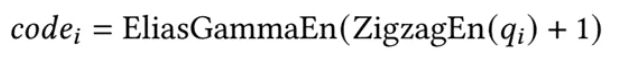
此处，ZigzagEn(q_i ) = (q_i<< 1) xor (q_i>> 63)，其中xor是按位异或运算。如果q_i= 0，那么ZigzagEn(q_i) = 0，因此我们需要额外加 1 以确保 Elias gamma 编码的输入为正数。假设N_i= ZigzagEn(q_i) + 1，Elias gamma 编码写入⌊log₂N_i⌋个零，然后附加N_i的二进制数字。例如，如果q_i= 5，那么N_i= ZigzagEn(q_i) + 1 = 11，其中⌊log₂N_i⌋= 3，并且N_i的二进制数字是(1011)₂。因此，code_i= EliasGammaEn(N_i) = (000 1011)_2。

解码器是编码器的逆过程。它首先使用Elias gamma解码方法解码code_i，然后使用Zigzag解码方法解码结果，即：

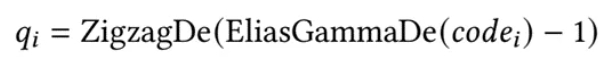
具体而言，Elias gamma解码首先读取并计数code_i的二进制数字中的零，直到遇到第一个1（假设零的计数为n_i），然后读取剩余的n_i位。首次读取的1和n_i位组合成解码结果。例如，如果code_i= (000 1011)₂，则零的计数n_i为3，因此除了已读取的1之外，我们还需要再读取3位，形成N_i= EliasGammaDe(code_i) = (1011)₂ = 11。之后，我们减去1以抵消前面公式(3)添加的1。假设x是Zigzag解码的输入数字，则ZigzagDe(x) = (x >>> 1) xor (−(x&1))。

2.1.3讨论

Serf-Qt速度极快，对于给定的值，其时间复杂度和空间复杂度均为O(1)。然而，Serf-Qt不支持相对误差有界压缩，因为公式（2）中，我们需要知道依赖于原始值的误差界限来进行相对误差有界压缩，而这是不可用的。此外，当ϵ_a很小时，Serf-Qt的性能会很差，因为根据公式 (1)，q_i会趋于变大。在极端情况下，如果ϵ_a足够小，q_i可能会溢出（即超出整数可以表示的范围），这使得Serf-Qt失效。

2.2 基于异或的方法Serf-XOR

为了解决Serf-Qt的问题，文章提出了一种基于异或运算的方法Serf-XOR。据调研这是第一个基于异或运算的有损浮点压缩方法。

2.2.1 主要思想

现有的基于异或的浮点压缩方法基于以下假设：时间序列中任意两个连续的值变化不大，因此它们的异或值往往包含许多前导零和尾随零。然而，这个假设并不总是成立。首先，如果两个连续的值具有不同的符号（例如，图3(a)中显示的-0.96和2.02），他们的异或值不包含任何前导零。其次，即使两个连续的值具有相同的符号，如果它们的指数表示形式有突变（例如，图3(b)中显示的0.98和2.09），则前导零仍然非常少。第三，在大多数情况下，尾随零实际上相当少（例如，图3(a)中没有尾随0，图3(b)中的2个尾随0）。前导零和尾随零的缺乏会导致较差的压缩性能。为此，我们提出一种移位技术来增加前导零，以及一种近似技术来增加尾随零。

图3. Serf-XOR的动机

图4给出了Serf-XOR的框架，它包含两个主要部分：Serf-XOR压缩器和Serf-XOR解压缩器。

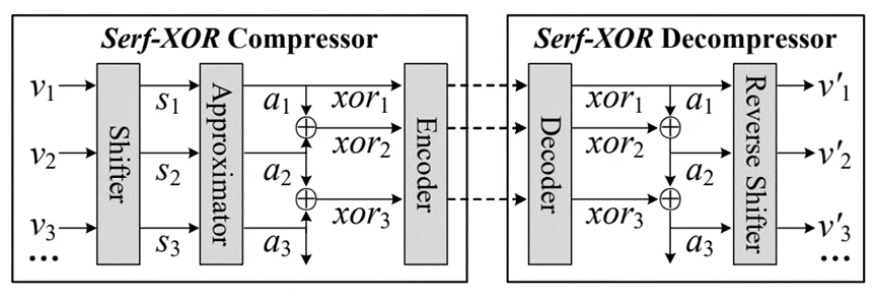
图4.Serf-XOR的框架

2.2.2  Serf-XOR压缩器

在 Serf-XOR 压缩器中，浮点数值 ⟨v₁, v₂,v₃ ...⟩ 依次流入移位器 (Shifter)，获得一个具有相同符号和相同指数的移位数值序列 ⟨s₁, s₂, s₃...⟩。之后，近似器(Approximator) 将移位数值逐一转换为近似数值序列 ⟨a₁, a₂, a₃...⟩。每个近似数值 a_i（除了第一个数值 a₁)）与其前一个数值  a_i-1执行异或 (XOR) 操作，从而产生一个具有大量前导零和尾随零的异或数值序列 ⟨xor₁,  xor₂, xor₃...⟩，该序列可以通过编码器 (Encoder) 进行压缩。

移位器：移位器给每个v_i增加一个整数偏移量λ，从而获得一个移位后的值s_i=v_i +λ，该值与其他移位后的值具有相同的符号（即正数）和相同的指数。因此，任何两个连续的移位后的值都可以产生一个具有许多前导零的异或值。但是如何确定一个合适的λ呢？

图5. 添加偏移量会导致信息丢失

一方面，λ应该足够大，以使所有s_i为正数并具有相同的指数。另一方面，如图6所示，添加偏移量可能会导致尾数右移，从而导致一些信息丢失。较大的偏移量通常意味着更多的信息丢失。在极端情况下，如果λ过大，s_i可能会溢出。为此，我们令λ为使所有s_i落在范围[2^u, 2^u+1)内的最小值，其中u是一个正整数，如图6所示。我们给出以下定理来找到 u和 λ。

图6. 位移器图示

定理 1。 给定一个时间序列TS=⟨v₁, v₂, ...⟩，假设 ∀v_i ∈TS，min ≤ v_i ≤ max。如果 u = ⌈log₂(⌊max⌋− ⌊min⌋ + 1)⌉ 且 λ = 2^u− ⌊min⌋，我们可以保证所有平移后的值s_i=v_i +λ都在范围 [2^u, 2^u+1) 内，并且λ同时是最小的。

近似器：在此模块中，对于每个位移值s_i，我们尝试找到一个近似值a_i∈ [s_i-ϵ,s_i+ϵ]，使得a_i和a_i-1共享最多的后缀位，即它们的异或结果具有最多的尾随零。这里，ϵ= ϵ_a（即，基于绝对误差界限）或ϵ=ϵ_r× |v_i|（即，基于相对误差界限）。

图9展示了近似器的基本思想，其中a_i-1= 2.535，s_i= 2.81，且ϵ= ϵ_a= 0.01。为了找到a_i∈ [s_i-ϵ,s_i+ϵ]，我们可以简单地将s_i的后45位设置为a_i-1的后45位，从而得到a_i = 2.800625（即，a_i由s_i的前19位和a_i-1的后45位组成，表示为a_i = pre₁₉ ⊢ suf₄₅。我们称s_i 为前缀锚点，a_i-1 为后缀锚点）。通过对a_i和a_i-1进行异或操作，我们可以得到一个异或值，该值具有许多前导零和尾随零。在解压缩期间，由于a_i∈[s_i-ϵ,s_i+ϵ]，我们有v_i'= a_i-λ∈[s_i-λ-ϵ,s_i-λ+ϵ]，即v_i'∈[v_i-ϵ,v_i+ϵ]，这满足误差界限的要求。下面介绍如何有效地找到一个合格的a_i。

一个直接的解决方案是迭代地检查a_i=pre_bn-j⊢ suf_j是否满足误差界限要求，其中j从bn到0，而bn是值的位数（例如，对于双精度值，bn=64）。如果是，则停止验证，并返回a_i。然而，可能存在两个问题。问题一：获得的a_i可能不是最优的（即，它与a_i-1)不共享最多的后缀位）。例如，在图8中显示存在另一个合格的2.81625 ∈[2.80, 2.82]，它与a_i−1共享的后缀位比图7中显示的2.800625更多。问题二：从头开始枚举所有后缀suf_j可能会花费大量时间，这会损害压缩效率。

图7. 基本近似器 (ε=ε_a=0.01)

图8. 优化后的近似器 (ε=ε_a=0.01)

为此，本文提出了一种新方法，以更有效的方式找到理论上最佳近似值a_i。为了解决问题一，文章采用了两种优化方法。首先，我们令前缀锚点为low=s_i-ε，而不是s_i。其次，除了检查连接c_i = pre_bn-j ⊢ suf_j是否在[s_i − ε, s_i + ε]中之外，我们还检查c₂ = (pre_bn-j + 1) ⊢ suf_j是否在[s_i − ε, s_i + ε]中。图9显示了三个连接的示例。在图11(c)中，我们发现c₂ = (pre₄ + 1) ⊢suf₁满足误差界限要求，因此我们最终设置a_i = c₂= (01100)₂。定理2可以保证这两种优化的正确性。

图9. 近似值搜索的示例（为简单起见，一个值的位数bn为5）

定理 2。假设low= s_i − ε是前缀锚点，且a_i-1是后缀锚点。如果我们迭代地检查两个连接c₁=pre_bn-j⊢suf_j和c₂= (pre_bn-j + 1) ⊢suf_j，其中j从bn到 0，我们总是可以获得一个合格的近似值a_i，它与a_i-1共享最多的后缀位。

在定理2中，迭代j共bn+1次（即，从bn到0）。但有时没有必要从头开始迭代j。具体而言，可以利用定理3来解决问题二。

定理 3。 假设low = s_i − ε，up =s_i + ε，且l = lead(low xor up)  是low xor up 的前导零的数量。如果我们从bn − l 到 0 迭代j，我们仍然可以获得最佳的a_i。

根据定理3，只需将j从bn − l迭代到0即可。由于ε通常非常小，因此low和up之间的差异通常很小，即l = lead(low xor up) 应该很大，这会显著降低迭代成本。例如，如图9所示，由于 lead(low xor up) = 2，我们从5 − 2 = 3开始迭代j，而不是从5开始。

编码器：为了编码异或后的值，我们采用了自适应编码策略，它包含近似规则的概念（一个排序的整数数组）。如图12(a)所示，假设前导零的近似规则为rule_lead= ⟨0, 8, 12, 16, 18, 20, 22, 24⟩，尽管前导零的数量是13，我们将其视为12（因为12 ≤ 13 < 16）。因此，前导零的数量可以用ln= ⌈log₂|rule_lead|⌉ = 3位（称为表示成本）来表示，而不是用⌈log₂65⌉ = 7位（前导零的数量可以是0∼64）。第13个前导零被认为是中心位的一部分，这会使中心位增加一位的成本（称为近似成本）。文献[1]提出了一种基于动态规划的方法，可以有效地找到表示成本和近似成本之间的最佳权衡。

图10(c)展示了xor_i = ai xor a_i-1 的编码策略，其包含三种情况。标志代码是根据每种情况的频率精心选择的。更多细节请参考[1]。

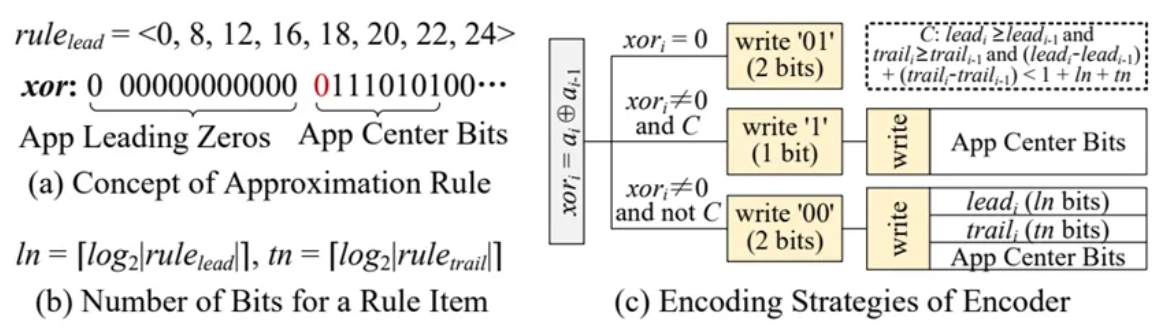
图10. 编码器的主要思想

算法1描述了Serf-XOR压缩器的伪代码，它以当前值v_i、上次近似值a_i-1（在我们的实现中，(a₀ = 0）、误差界限ε、前导/尾随零的近似规则rule和流写入器out作为输入。在第17行，我们在每个窗口（例如，1,000个值）的末尾更新并写入规则，以便在后续压缩中获得更好的近似规则。

我们最多迭代bn− l 次，因此其时间复杂度为 O (bn − l)。我们需要存储前导/尾随零的统计信息（用于更新近似规则），其中包含不超过2 × bn条记录，因此算法1 的空间复杂度为 O (bn)。

2.2.3  Serf-XOR解压缩器

如图5右侧部分所示，在Serf-XOR解压缩器中，压缩的比特流被送入解码器，得到一系列异或值⟨xor₁, xor₂, xor₃, ...⟩，通过异或运算，我们可以得到近似值⟨a₁, a₂, a₃...⟩。反向移位器将每个a_i转换为浮点数值v_i'。解压缩器并非压缩器的严格反向过程。

如算法2所示，Serf-XOR解压缩器以最后一次近似值a_i-1、近似规则rule和输入流读取器in作为输入。第1∼12行是解码器的代码。由于标志代码可以是‘1’、‘00’或‘01’，我们首先读取一位。如果它是‘0’，我们需要再读取一位来组装标志flag。随后，我们根据标志flag的值分别处理这三种情况，最后在第12行获得近似值a_i。在第13行，反向移位器计算解压缩值v_i'=a_i-λ。与Serf-XOR压缩器类似，如果需要，我们需要在每个窗口的末尾读取和更新规则rule，以便后续解压缩。

由于算法 2 中没有任何循环，因此其时间复杂度为 O(1)。此外，我们只在内存中保留几个状态（例如，lead_i-1和trail_i-1），因此空间复杂度为 O(1)。

三．实验

3.1实验设置

数据集.  采用了来自不同领域的13个时间序列数据集，这些数据集具有不同的采样间隔。从每个数据集中随机提取最多100,000个连续记录。此外，采用时间序列基准中的数据集来验证所提出方法的稳健性。

基线方法. 我们将 Serf 与 17 种具有代表性的竞争方法进行比较，包括 4 种批处理无损方法（即 LZ77、Zstd、ALP 和 Snappy）、7 种批处理有损方法（即 SZ2、Machete、Sim-Piece、SZ_ADT、Sprintz、HIRE 和 Buff）以及 6 种流式无损方法（即 Deflate、LZ4、FPC、Gorilla、Chimp128和 Elf）。对于批处理方法，在小批量中运行它们。Deflate 和 Zstd 设置为默认压缩级别，而 LZ77 设置为压缩级别 2，以获得更好的压缩率。

 度量标准. 通过三个主要指标验证各种方法的性能：压缩率、压缩时间和解压缩时间。压缩率定义为压缩数据大小与原始数据大小的比率。

3.2 总体比较

使用绝对误差界限ε_a= 0.001在每个数据集上运行每种方法，并报告一批次50条数据记录的平均性能。

表2. 总体比较-压缩率

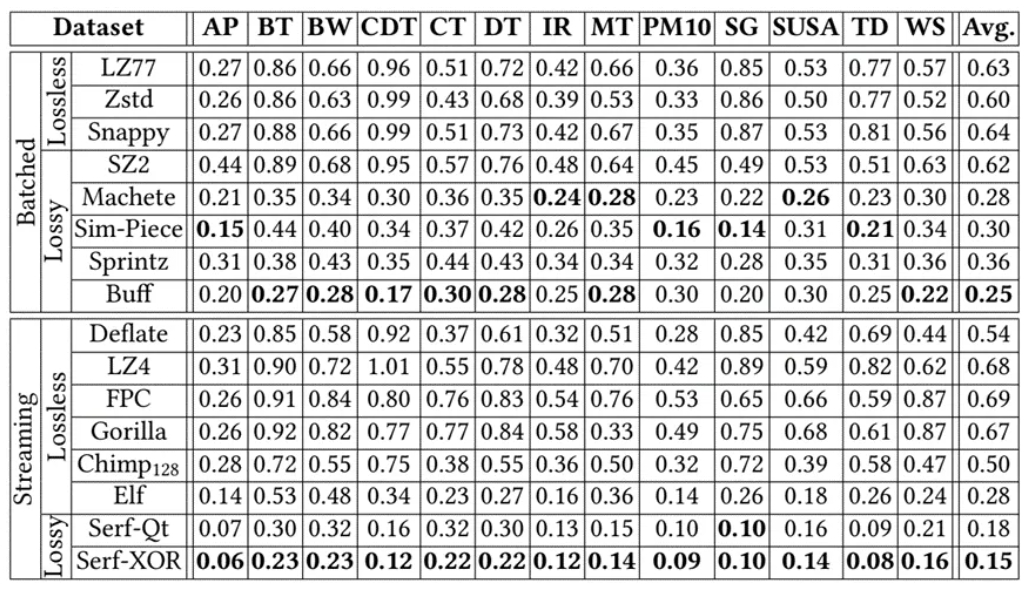
可以看到，在所有方法中，Serf在所有数据集上始终具有最佳压缩率。Buff在批式方法中显示出最佳压缩率（即0.25），但它只能支持格式为10^−k的误差范围，并且Serf-XOR仍然比它平均有40%的相对改进。并且Serf-XOR 的压缩率略优于 Serf-Qt。

表3. 总体比较-压缩时间（us）

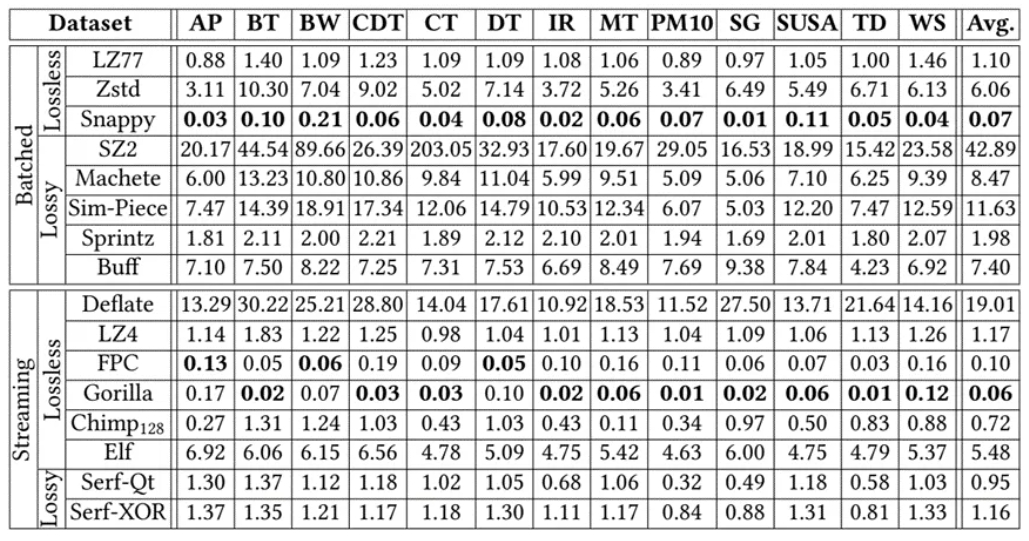
表4. 总体比较-解压时间（us）

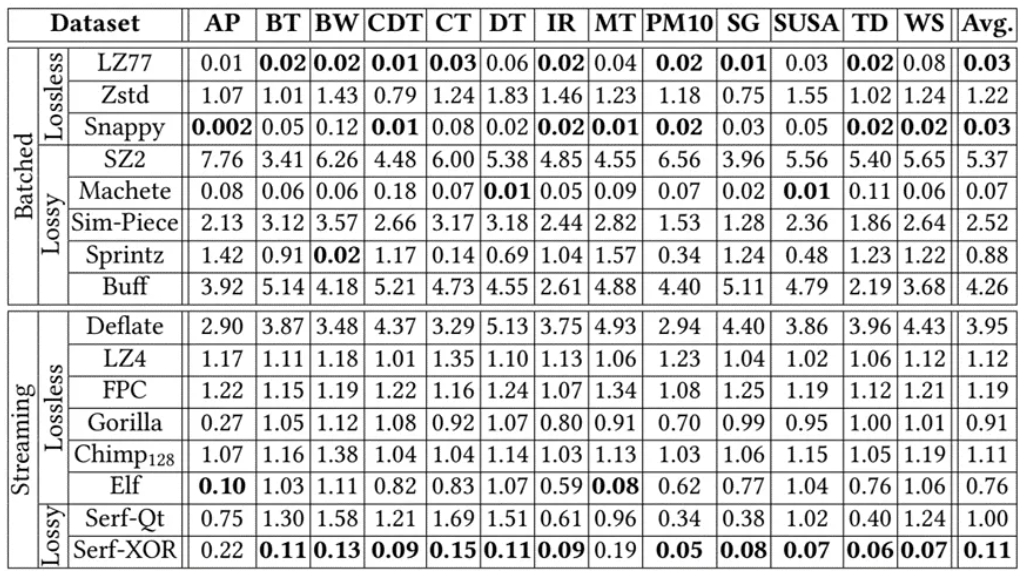
虽然Serf在压缩时间上表现并不是最好的，但是流式压缩中，压缩时间最短的Gorilla的压缩率低至0.67，约为Serf-XOR的4.47倍。这在带宽有限的场景中十分不利。而压缩率最高的Elf，压缩时间比Serf更多。而解压缩方面，Serf-XOR在一些类别中有最佳表现。

3.3 流式传输实验

为了验证所提出的方法在流数据传输场景中的整体性能，我们基于一个真实的开发板Dofly CC2530构建了一个流式传输原型系统。将Dofly CC2530光敏传感器的采样率分别设置为从0.1kHZ到18kHZ，并基于Zigbee通信协议，观察从传感器向服务器传输100,000条记录时，使用不同流压缩方法所花费的总时间（包括压缩时间、传输时间和解压缩时间）。在不同的采样率下，Serf-XOR总是花费最少的时间，因为它具有最佳的压缩率，从而有助于传输最少的比特。

实验证明了所提出的方法在带宽受限的流数据传输中的可行性。

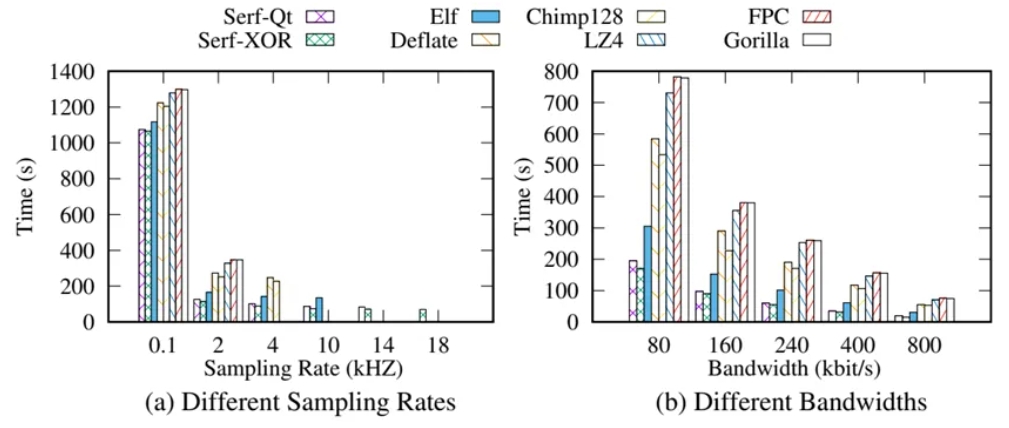
图11. 数据传输实验

3.4其他主要实验

不同ε_a下的性能. 实验逐步将ε_a从10⁻¹变化到10⁻⁶。所有方法的压缩率都呈现上升趋势。在所有有损压缩方法中，Serf-XOR始终具有最佳的压缩率。随着ε_a的减小，Serf-XOR相对于Serf-Qt在压缩率方面的优势更加明显。

不同批处理大小下的性能. 批处理大小从50到800不等。随着批次大小的增加，所有方法都需要更长的压缩时间。但Serf-XOR和Serf-Qt在所有小批次大小中都具有最具竞争力的压缩效率。

四．总结

论文提出了首个流式误差有界浮点压缩算法Serf。它由基于量化的Serf-Qt和基于异或的Serf-XOR组成，两者都在流式场景中具有显著的压缩率和高效率。对于Serf-XOR，论文提出了一种新颖的数据偏移技术，以增加异或值的先导零，其中最佳偏移量可以通过严格的理论指导来计算。并提出了一种新颖的近似技术，用于寻找与先前近似值共享最多“尾部”位的误差限定近似值，从而产生具有许多尾随零的异或值。我们进一步提出了一种剪枝策略，以加速近似值搜索的过程。作者使用来自不同来源的13个时间序列，将Serf与17个最先进的竞争对手进行比较，表明Serf在流式传输场景中实现了最佳压缩率。并且在基于真实的开发板Dofly CC2530构建了一个流式传输原型系统中，当带宽受限时，Serf始终占用最少的总时间。

参考文献：[1] Zheng Li, Ruiyuan Li*, Xiaolong Xu, Yi Wu, Chao Chen, Tong Liu, Jiaxing Shang, Yu Zheng. Adaptive Encoding Strategies for Lossless Floating-Point Compression. IEEE Internet of Things Journal. (IoTJ, SCI 1区)

本文作者 周钦钦 西南交通大学软件工程2021级本科生，重庆大学Start   Lab团队成员。 主要研究方向：轨迹数据压缩

重庆大学时空实验室（Spatio-Temporal Art Lab，简称Start Lab），旨在发挥企业和高校的优势，深入探索时空数据收集、存储、管理、挖掘、可视化相关技术，并积极推进学术成果在产业界的落地！年度有3~5名研究生名额，欢迎计算机、GIS等相关专业的学生报考！

关注公众号，回复“Serf”获取论文及源码

       

              图文｜周钦钦

              校稿｜李   政

              编辑｜李佳俊

              审核｜李瑞远

              审核｜杨广超